Brevissimi cenni sull’universo dell’Algebra… del suocero di Wilfrid Voynich…e del famosissimo Manoscritto M408; di Roberto Volterri

 

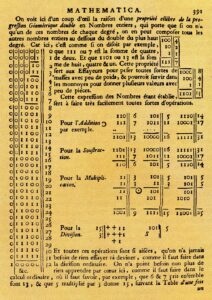
Immagine di apertura; Un bellissimo libro di Ruggero Bacone (Roger Bacon), stampato ad Amsterdam nel 1660. Avrebbe fatto felice personaggi  come Voynich, Kraus e… anche noi!

 

Brevissimi cenni sull’universo dell’Algebra… del suocero di Wilfrid Voynich…e del famosissimo Manoscritto M408

di Roberto Volterri 

Confessiamo apertamente di non essere affatto esperti in lingue “inventate” e ci cospargiamo il capo di cenere per conoscere soltanto l’idioma di chi passeggiava all’ombra del Colosseo una ventina di secoli fa, magari insieme al greco antico, ad un po’ di fenicio e consistenti rudimenti di lingua etrusca.

Però il “Manoscritto Voynich” è intrigante non solo per le stranissime immagini in esso riportate – in particolar modo quelle con le allegre fanciulle intente a fare salutari abluzioni – ma anche per i curiosi caratteri che costituirebbero un linguaggio articolato, dotato di una sua sintassi, di sue regole grammaticali.
O almeno così sostiene chi si è avventurato nel “tradurre” la strana lingua che fa da contorno a curiose piante, a esistenti o inesistenti costellazioni, ad una idroterapia ante litteram…

Dunque, approfittando del fatto che “semel in anno licet insanire”, sapendo che Ethel Voynich era non solo la moglie del notissimo mercante di libri antichi ma era anche la figlia di un grande matematico, George Boole (1815 – 1864), al quale dobbiamo l’algebra booleana e l’esistenza stessa del PC con il quale stiamo scrivendo queste “follie”, ebbene, durante un’agitata notte… siamo “impazziti”.

Ci è venuto in mente che l’intraprendente personaggio il quale, molti anni più tardi – Boole morì quando sua figlia Ethe Lilian, detta anche “Lily” aveva poco meno di un anno – sarebbe convolato a giuste nozze con la figlia del grande matematico, avrebbe potuto trovare spunto proprio da tale particolarissima algebra per ideare un metodo atto a codificare una strana lingua mediante “lettere” che nel loro insieme potrebbero costituire delle “stringhe” basate sulle cifre 0 e 1, su ON e OFF.
Insomma sulla lingua che è la base dell’informatica moderna.
Tutto ciò, ovviamente nella “folle” ipotesi del falso recente…
Ora facciamo un passo indietro nel tempo e rechiamoci… in Cina.

L’Algebra di George Boole. Suocero di Wilfrifd Voynich…

‘Acceso’ o ‘Spento’, ON e OFF, ‘Alto’ e ‘Basso’ sono termini usuali per chi si occupa di elettronica digitale basata appunto sull’Algebra di Boole.
Al grande matematico irlandese George Boole – repetita iuvant… suocero di Voynich! – deve essere riconosciuto il merito di aver costituito un complesso sistema algebrico capace di un’interpretazione puramente qualitativa, sistema che – ad onor del vero – come più avanti vedremo, trova in Leibniz (1646 – 1716) uno dei più geniali precursori con lo scritto ‘De Progressione Dyadica’ del 1679.

2. Immagine sopra; Il grande matematico George Boole, suocero di Wilfrid Voynich e creatore dell’algebra che da lui prende il nome.

Una cosa, riguardo Leibniz, è importante rilevare: il filosofo e matematico era in contatto epistolare con padre Joachim Bouvet, gesuita e missionario in Cina, terra in cui almeno quattro millenni or sono fu creato ‘L’Oracolo delle Mutazioni’, più noto come Libro dei I-Ching.

3. Immagine sopra; Il gesuita Joachim Bouvet che inviò al matematico Leibniz informazioni sugli esagrammi del “Libro dei Mutamenti” o I-Ching e da tutto ciò nacque, dopo l’intervento di George Boole – suocero di Voynich – l’algebra che costituisce la base per la programmazione di ogni apparecchiatura elettronica digitale, compreso il vostro PC!

4. Immagine sopra; Gottfried Wilhelm von Leibniz (1646 – 1716), il grande filosofo e matematico che seppe intuire le applicazioni degli esagrammi dell’I-Ching.

Padre Bouvet aveva a lungo studiato la filosofia cinese, il Taoismo e il Confucianesimo ed aveva avuto modo di apprezzare la profondità di pensiero che si celava dietro quello strano metodo di ‘scrutare’ il futuro o, meglio, di comprendere il vero rapporto tra l’inconscio, la complessa realtà e… il caso.
L’I-Ching, o Libro dei Mutamenti, rappresenta una tra le più rilevanti opere della cultura cinese. E’ stato attribuito all’imperatore mitico Fu-Hsi, anche se alcuni studiosi lo datano – più verosimilmente – verso l’anno 1000, tra la Dinastia Shang e la Dinastia Chou.

Secondo alcune tradizioni, l’I-Ching ebbe alcune evoluzioni a partire dai primi otto trigrammi di Fu-Hsi divenuti i sessantaquattro esagrammi di Yu-Li comprendenti anche le modifiche apportate dal Duca di Chou verso il 1100 a.C.
Altre fonti affermano che tra i primi a studiare l’I-Ching ci fu il re Wan, capostipite leggendario della Dinastia Kau.

Sempre intorno al XII secolo a.C. egli, mentre si trovava imprigionato per aver cospirato contro la potente famiglia Yin, incominciò ad annotare sue riflessioni sulla possibile interpretazione degli esagrammi.
A parte i rapporti tra padre Bouvet e Leibniz, il Libro dei Mutamenti trovò ampia diffusione in Occidente solo dopo la traduzione in inglese fatta dal sinologo James Legge verso la fine del XIX secolo. Successivamente apparvero le traduzioni in tedesco di Richard Wilhelm – verso la fine degli Anni Trenta del XX secolo – e ancora in inglese da Cary Baynes (nato Cary Fink, 1883-1977).

5. Immagine sopra; Medaglia progettata da Leibniz per meglio stigmatizzare i vantaggi della numerazione binaria rispetto a quella decimale

Nota, soprattutto per le ‘istruzioni per l’uso’ è la versione in inglese di John Blofeld apparsa intorno agli Anni Sessanta dello scorso secolo.
Non ci dite ora che non trovate analogie tra la linea intera degli esagrammi – chiamata Yang, ma che potremmo anche chiamare… ON – e la linea spezzata, chiamata Yin, ma che si potrebbe chiamare anche… OFF?
Ebbene padre Bouvet, avendo inviato a Leibniz il testo dei I-Ching forse mutò radicalmente il corso della storia!

Leibniz, infatti, studiò per giorni e giorni i sessantaquattro esagrammi e, da grande matematico quale era intuì subito che una combinazione di quelle linee intere, di quelle linee spezzate poteva rappresentare qualsiasi numero con una logica non più ‘decimale’ ma ‘binaria’.
Dette quindi alle stampe il suo lavoro ‘Explication de l’arithmétique binaire’, pubblicato a Parigi nel 1703, in cui esponeva i vantaggi del calcolo con logica binaria rispetto a quello basato sul sistema decimale.

6. Immagine sopra: ‘Explication de l’arithmétique binaire’, pubblicato da Leibniz a Parigi nel 1703, in cui egli esponeva i vantaggi del calcolo con logica binaria rispetto a quello basato sul sistema decimale.

Come già accennato, venne poi George Boole che – a metà dell’Ottocento – pubblicò un suo scritto di logica matematica, basato sulle ‘riflessioni’ di Leibniz, intitolato curiosamente ‘Investigazione sulle leggi del pensiero’.

Non è certamente questa la sede adatta per… confondere le idee ai lettori con ‘semplici’ concetti come quello di ‘Reticolo di Bole’, di ‘sottoinsiemi non vuoti’ o di ‘omomorfismo booleano’, ma certamente non è possibile non ricordare che la particolare ‘algebra booleana’ trovò pratica applicazione solo quando si riuscì a creare dei dispositivi elettrici che simulassero le due condizioni di ‘ON’ e ‘OFF’, di ‘Acceso’ e ‘Spento’!

7. Immagine sopra; I sessantaquattro esagrammi cinesi del “Libro dei Mutamenti”. La linea spezzata può rappresentare la cifra 0, oppure lo stato OFF di un circuito elettronico impiegato in un Computer. La cifra 1, oppure lo stato ON, è invece rappresentata dalla linea continua.

 

Un calcolatore numerico opera infatti con numeri rappresentati al suo interno per mezzo di sistemi ‘bistabili’, capaci cioè di assumere soltanto due ben determinate condizioni: ON e OFF.

Nell’algebra binaria, tanto per fare un esempio, una serie di 0 e di 1 come…
10011101

corrisponde al numero 157, espresso dalla somma di otto potenze di 2:

1 x 27 + 0 x 26 + 0 x 25 + 1 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20

Con lo stesso sistema è possibile esprimere praticamente qualsiasi numero ed effettuare moltiplicazioni, divisioni, addizioni, sottrazioni, oppure rappresentare qualsiasi lettera di qualsiasi alfabeto come ogni Personal Computer… dimostra!

L’Algebra di Boole, in realtà, non trovò pratica applicazione finché la tecnologia non mise a disposizione dei ricercatori dei dispositivi in grado di simulare gli stati logici 0 e 1. Negli Anni Quaranta del secolo da poco trascorso si pensò di simulare tali stati con i relais elettromeccanici: quando il relais veniva eccitato con l’applicazione di una tensione ai capi del solenoide che lo costituiva, il campo elettromagnetico generato attirava un’ancoretta mobile che chiudeva un contatto. Ciò simulava lo stato ON, cioè Acceso.
Quando la tensione di eccitazione veniva tolta, il campo elettromagnetico veniva a mancare, l’ancoretta mobile si rialzava e il contatto si apriva.

Tutto ciò simulava lo stato OFF, cioè, Spento.
Naturalmente effettuare delle complesse operazioni con tale sistema elettromeccanico era estremamente complesso, rumoroso e soprattutto lento.
L’avvento dei tubi elettronici – sì, delle care vecchie ‘valvole’ della ‘radio della nonna’ – aumentò la velocità di esecuzioni delle varie operazioni ma non ridusse di molto le dimensioni dei calcolatori che necessitavano di grandi ambienti e di sistemi per l’eliminazione della grande quantità di calore emessa di tubi elettronici stessi.
Poi – negli Anni’Sessanta – ebbe notevole sviluppo la tecnica dei semiconduttori, dei Transistor che simulavano molto più efficacemente gli stati logici ON e OFF e, soprattutto, consentivano di ridurre drasticamente le dimensioni del calcolatore.
L’avvento dei Circuiti Integrati – tra gli Anni Settanta e la fine degli Anni Ottanta – permise di ridurre le dimensioni di un Calcolatore, di un Computer, quasi a quelle attuali e con prestazioni ben lontane da quelle dei ‘primordi’.
I ‘microchips’ attuali lasciano letteralmente sbalorditi per le ridotte dimensioni, per le elevatissime velocità di calcolo, per i ridotti consumi di energia e per la velocità… con cui ‘invecchiano’ rapidamente, costringendoci ad acquistarne uno nuovo ogni due anni circa.
Certamente non tutti i sessantaquattro esagrammi dell’I-Ching trovano corrispondenza con il codice binario basato su condizioni ON e OFF, ma è estremamente interessante notare come lo stesso principio di funzionamento degli attuali Computer sia stato in tempi remotissimi applicato a metodi che sarebbe riduttivo definire esclusivamente ‘divinatori’ come il ‘Libro dei Mutamenti’.
Fine di quest’altra, brevissima… “lectio magistralis” che, speriamo, non vi abbia annoiati più di tanto!

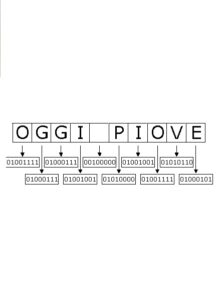
8. Immagine sopra; Una qualunque frase, ogni lettera di un qualunque linguaggio possono essere codificate ricorrendo alla logica binaria, all’algebra del matematico George Boole, padre di Ethel, moglie dell’ineguagliabile Wilfrid Voynich…

Nella lingua che, insieme alle immagini, costituisce l’essenza del Manoscritto MS408 sembrano – ma solo sembrano, si badi bene! – apparire simboli ricorrenti in modo periodico…

9. Immagine sopra; Esiste sul serio una periodicità o pseudoperiodicità nella presenza degli strani caratteri di ogni rigo del “Manoscritto Voynich”?

Tali scritte possono essere paragonate a “stringhe di testo” ìntese dal punto di vista della logica simbolica, dell’algebra che dobbiamo al suocero di Voynich, il matematico George Boole.

 

 

Riappare il “Doctor Mirabilis”!

Ebbene sì, riappare poiché Ruggero Bacone è stato il primo ad essere stato indicato come il possibile autore del “Manoscritto Voynich”.
Ovviamente nell’ipotesi che esso sia stato veramente realizzato nel XV o giù di là e non “in tempi molto più recenti”…
Già ne faceva cenno Johannes Marcus Marci in una lettera indirizzata a Kircher per chiedere “lumi” sul manoscritto venduto a caro prezzo a Rodolfo II d’Asburgo.

Date un’occhiata alla parte finale di una lettera – riportata al completo in altra parte di questo libro – in cui il gesuita Johannes Marcus Marci, da Praga, scrive a Kircher ipotizzando lo “zampino” del “Doctor Mirabilis”…
Ma era sul serio lo stesso manoscritto che ora è conservato a Yale?

 

… Il dottor Raphael, medico di Ferdinando II re di Boemia, colui il quale ha presentato il libro a Rodolfo II, ha avuto 600 ducati, affermando inoltre che l’opera è di Ruggero Bacone, ma qui mi astengo nel dare un giudizio.
Fatemi sapere cosa pensate di questa affermazione e, ringraziandovi, rimango in attesa …
Johannes Marcus Marci
Praga 19 Agosto 1665”

 

Il “Doctor Mirabilis” nasce in Inghilterra, a Ilchester nel 1214 da una famiglia benestante. Verso l’anno 1233 abbraccia la vita religiosa in ambito francescano e successivamente entra a far parte del corpo docente dell’Università di Oxford. Profondamente convinto che solo tramite il metodo scientifico – qualche secolo dopo lo definirebbero “galileiano”… – si possa procedere nel cammino della Conoscenza, non disdegna affatto di interessarsi di Alchimia e Astrologia.⁰

10. Immagine sopra; una statua dell’Università di Oxford (UK), raffigurante iI frate Francescano Ruggero Bacone (Fonte Wikipedia), da alcuni ritenuto l’autore delle pergamene conservate presso l’Università di Yale (USA).

Ruggero Bacone si trasferisce in Francia, a Parigi al’epoca fulcro della vita intellettuale di tutta l’Europa. Compone il trattato Opus Maius in cui espone le sue innovative idee nel campo della matematica, dell’ottica, dell’astronomia ed espone – quasi mostrando doti di preveggenza – l’invenzione del microscopio, del telescopio, di macchine volanti, di navi che solcheranno il mare spinte dalla forza del vapore.

Quasi un Athanasius Kircher molto ante litteram!

Però non è questa la sede più adatta per magnificare le doti intellettuali di Ruggero Bacone, ma è la circostanza migliore per riferirci ancora una volta alla “blasfema” – per buona parte di chi si interessa al “Manoscritto Voynich”.

Lo confessiamo, un po’ a malincuore… noi compresi! – ipotesi che il “libro più misterioso del mondo” possa aver preso vita in tempi ben lontani da quelli in cui visse il “Doctor Mirabilis”.

Magari proprio prendendo spunto da quanto egli aveva esposto nell’opera “De dignitate augmentatis scientiarum” del 1623 e basandosi su una algebra booleana che ancora… non esisteva ma che sembra intuibile nella raffigurazione di una pagina dell’opera di Bacone appena citata.

Se sostituiste le due lettere a e b con le cifre 1 e 0 caratteristiche dell’Algebra booleana potreste tradurre in codice binario “a cinque bit” qualsiasi testo.
La cosa strana è che la raffigurazione che trovate in queste pagine è tratta da un’opera di Ruggero Bacone, vissuto nel XIII secolo!

11. Immagine sopra;  iI frate Francescano Ruggero Bacone

 

 

 

12. Immagine sopra; Se sostituiste le due lettere a e b con le cifre 0 e 1 –
come sotto riportato – otterreste una numerazione in codice binario a cinque bit, secondo l’Algebra ideata da George Boole, suoccero di Wilfrid Voynich. Un caso, naturalmente…

 

 

                 A       B      C

D              E        F
            11111 11110 11101

11100 11011 11010

                G       H         J

K              L       M
             11001 11000 10111

10110 10101 10100   

                N        O        P

Q              R        S
             10011 10010 10001

10000   01111  01110

                T         V       W

X             Y          Z
              10010 10011 10100

10101  10110  10111

Ecco fatto! Dando il valore 1 alla lettera “a” e il valore 0 alla lettera “b”, la tabella ideata da Ruggero Bacone si trasforma automaticamente in una tabella in cui c’è una corrispondenza biunivoca tra le lettere dell’alfabeto latino e una pseudo-numerazione binaria a cinque bit.
Forse, né all’epoca del “Doctor Mirabilis” , né all’epoca di Boole, di sua figlia Ethel, di suo genero Wilfrid Voynich e di Krauss Co., sarebbe stato difficilissimo dar vita ad un antico manoscritto “cifrato” con “caratteri pseudobooleani”…

 

Se così fosse, se veramente – dopo un’accuratissima analisi dello strano linguaggio – emergesse una ricorrenza periodica di “lettere” riconducibili ad una sorta di plausibile algebra binaria, si potrebbe tentare di enucleare dal testo del “Voynich” la presenza di vere e proprie “stringhe di testo scritte mediante una logica simbolica e – con una buona esperienza nella programmazione di PC, del “linguaggio macchina” basato su un alfabeto binario costituito dai soli simboli numerici 0 e 1 – forse sarebbe possibile tradurre dette “stringhe” in un linguaggio comprensibile anche dall’entità biologica Uomo.

Comprensibile, quindi, non solo dal “cretino ad altissima velocità” come il Computer fu definito dallo scrittore Luca Goldoni, poi chiosato da Stefano Benni il quale, alla frase, aggiunse “… in dotazione, spesso, a cretini molto lenti”!

Oltre tale “folle” ipotesi di lavoro, non volendo correre il rischio di essere annoverati nella categoria “benniana”… non desideriamo (per ora) andare oltre!
Però, nel caso vogliate dilettarvi a tradurre qualsiasi testo, di qualsiasi lingua, in codice binario “a otto bit” provate ad andare sul sito:

http://guardacqua.it/risorse/binario

Ad esempio, digitando Wilfrid Voynich & Hans Peter Kraus nel riquadro dove c’è scritto “Testo normale”, immediatamente, nel riquadro sottostante apparirà la “traduzione” in codice binario “a otto bit” qui riportata…

01010111 01101001 01101100 01100110 01110010 01101001 01100100 00100000 01010110 01101111 01111001 01101110 01101001 01100011 01101000 00100000 00100110 00100000 01001000 01100001 01101110 01110011 00100000 01010000 01100101 01110100 01100101 01110010 00100000 01001011 01110010 01100001 01110101 01110011 00100000

 

 

13.  Immagine sopra; C’è, però, anche chi pensa di avere trovato la perfetta corrispondenza tra le “lettere” del “Voynich” e alfabeti d’uso comune…

 

(Roberto Volterri)

14. LA COPERTINA DEL NUOVO LIBRO DI ROBERTO VOLTERRI E BRUNO FERRANTE!!!!

Amazon, Dicembre 2024. Con un centinaio di immagini a colori.

 

Tratto da recensioni pubblicate.
“… Attraverso l’entusiasmo degli Autori nel raccontare le vicende legate al cardinale Flavio Chigi e alla tradizione delle “Statue parlanti” di Roma, il libro si trasforma in un viaggio intrigante nel XVII secolo, rivelando connessioni uniche tra la vita quotidiana a Formello – ameno paese a due passi da Roma – e le dinamiche sociali dell’epoca. La fusione di immaginazione e realtà aggiunge uno strato narrativo affascinante. Le testimonianze raccolte e il richiamo ai “grilli parlanti” di Formello contribuiscono a evidenziare il ruolo sociale e comunicativo della statua del Maripara, rendendo il libro non solo un resoconto storico, ma anche una riflessione sulla persistenza di forme di critica sociale nel corso del tempo…”
“… Il “Maripara” Era ed è una sorta di ermafrodita che una volta assomigliava ad un Priapo “itifallico” mentre mostrava a tutti i paesani i suoi attributi maschili. Poi, nel corso di poco più di un secolo, molte cose sono cambiate ed ora, nel bel Museo dell’Agro Veientano di Formello, potete ammirare il cosiddetto Maripara restaurato, anche se ha perso alcune delle sue peculiarità che scandalizzarono gli abitanti (e le abitanti…) dell’ameno paese a due passi da Roma.”

15.  Immagine sopra; il professor Roberto Volterri.

 

– se non altrimenti specificato, le immagini sono state fornite dall’autore